Chapter One: An Acoustics Primer

5. What is frequency?
The number of cycles per unit of time is called the frequency. As mentioned in the previous section, the period (unit of time per cycle) is the reciprocal of the frequency. For convenience, frequency is most often measured in cycles per second (cps) or, equivalently, hertz (Hz), so 60 cps = 60 Hz (named after the 19th-century physicist Heinrich Hertz). As is customary, the fully-named unit is all lower case, and the symbol is capitalized. One thousand Hz is often written as 1 kHz (kilohertz) or simply '1k' in studio parlance. And, of course, a single cycle is still 1 hertz, not 1 hert!
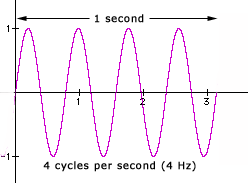
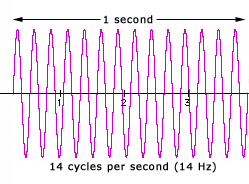
Ultrasonic frequency ranges: One million hertz is referred to as 1 MHz (megahertz), and one billion hertz is 1 GHz (gigahertz). Neither MHz nor GHz are normally part of audio applications, as human hearing typically extends to 20 kHz at best. In fact, sound in air has a frequency limit due to propagation laws. The highest airborne acoustic frequency produced and recorded as of this writing is 10 GHz, and these waves travel extremely short distances before dying out. Medical ultrasounds range from 2 MHz to 15 MHz and travel through solids and liquids, not air. GHz—perhaps terahertz someday—are relevant when selecting a computer by processor clock speed. My personal favorite SI frequency band (being a Seinfeld fan) is the yottahertz (YHz), which is 1024 Hz.
ANOTHER METHOD: angular velocity (ω)
An additional method for quantifying frequency, used extensively in signal processing math, such as phase vocoding and STFT calculations, entails measuring the angular velocity of the signal, or the rate of change of angular displacement, represented by the Greek letter theta (θ). In this case, the angular velocity is simply the rate of phase rotation represented by a point on the circumference of the counterclockwise (CCW) spinning disk. The video above represents a single cycle of a sine wave traced via rotational change (disk) versus time. Angular velocity is usually denoted by the Greek lowercase letter omega (ω) and represents the rate of rotation, such that an entire cycle is equal to a rotation of 2π radians (equivalent to 360°). ω is normally expressed as radians per second or rad/s. ω as rad/s is equivalent to 2πƒ expressed in Hz (cps). So 1 Hz would be ω ≈ 2π (~6.3) rad/s, and 60 Hz would be ω ≈ 377 rad/s.
For further study, see Hyperphysics: Angular Velocity