Chapter One: An Acoustics Primer

7. What is amplitude? | Page 4
Decibels: Definition, decibels that measure power and intensity
While power is measured in watts, a widely used measurement unit for relative amplitude, power, intensity, sound pressure at the listener, and comparative voltage from a microphone is the decibel (dB). Named in honor of Alexander Graham Bell, the measurement was derived from a scale originally used to determine signal loss in telegraph and telephone lines, known as the bel. To avoid fractional values of the larger bel, the decibel—one tenth of a bel—became the standard. A decibel is a logarithmic measurement that reflects the vast range of sound intensity our ears can perceive and closely correlates to the physiology of our ears and our perception of loudness. There are many different forms of decibel measurement, and it is not always clear which method of computation is being used. However, specific labels often indicate the method or reference value, such as dBm, dBV, dB SPL, dB SIL, dB SWL, dBFS, dBu, dBVU. Additionally, scale weightings such as dB(A) and dB(C)—often found on sound level meters—will be examined later in this text.
Ambiguity abounds in dB labeling, so take care that you know what is being measured and the reference benchmarks being used. The SI (International System of Units), ISO and others do not recognize any of the suffixes above for decibels, and in literature, the letter p is often used in dB equations to represent power, pascals, or pressure, which are NOT interchangeable, so mind your p's if not q's.
To get started, a brief review of logarithms (often misspelled by musicians as logarhythms) is in order.
Do not be intimidated by calculating logarithms. With modern calculators to perform the math (where one previously used log tables), a simple understanding of the concepts is sufficient for decibel calculations.
\(\log_{10} x\) can be thought of as "what power of 10 will result in x?" For example, \(\log_{10} 100 = 2\) because \(10^2 = 100\).
Decibels are often used to measure very minute values, which can also be expressed by logs of decimal numbers or their negative power equivalents, e.g., \(x^{-y}\).
For example, \(\log_{10} 0.1 = -1\) and \(\log_{10}\) \(0.000000000001 = -12\) because \(10^{-12}\) = \(0.000000000001\). This value will be used for the threshold of hearing measurement below.
If a log is expressed \(y = \log_{10} x\), then \(10^y = x\).
Decibels
A decibel is a unit used to compare the ratio of power, intensity, or amplitude between two acoustic sounds or electronic signals. The ratio (R) of two signals expressed by their power in watts, \(W_1\) and \(W_2\), is:
\[ R = 10 \log_{10}\!\left( \frac{W_1}{W_2} \right) [\text{dB}] \]
A doubling of power equals an increase of +3 dB (try it out with the formula above). When we study filters later on, note that a filter cutoff frequency is defined as the half-power point, which is calculated as –3 dB.
Decibels that measure power and intensity
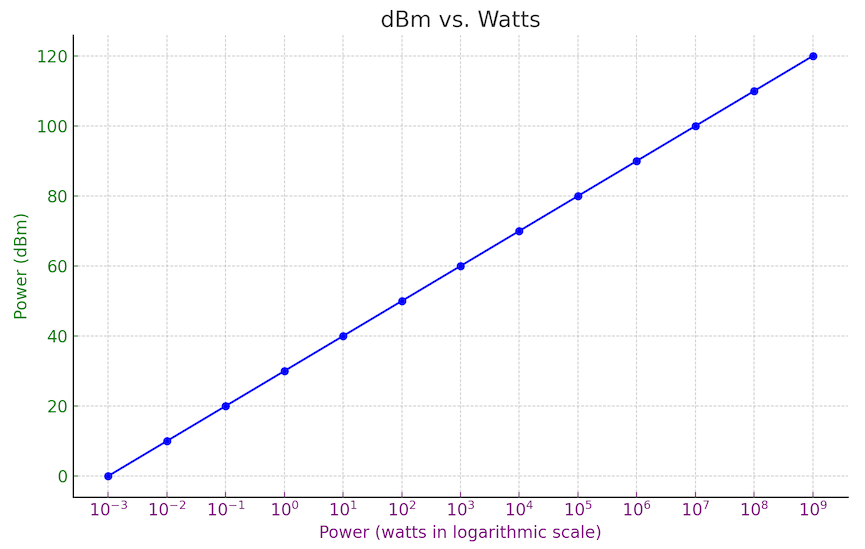
There are many different types of decibel measurements, so for clarity, the formula above, which measures power or intensity, yields dBm when a fixed reference value of 1 milliwatt is used for the denominator. dBm is the form most commonly used to evaluate power in audio circuits. To establish a standardized absolute measurement of power in an electronic circuit (i.e., a comparison to an industry-fixed value rather than another signal), the nominal reference power \(W_{2}\) is defined as 1 milliwatt (0.001 watt). In absolute terms, a 1-watt signal—which has 1,000 times the power of the reference value—will measure 30 dBm, as calculated below:
\[ \begin{aligned} \mathrm{dBm} &= 10\log_{10}\!\left(\tfrac{1\,\mathrm{W}}{0.001\,\mathrm{W}}\right)\\ \mathrm{dBm} &= 10\log_{10}(1000)\\ \mathrm{dBm} &= 10 \times 3 \quad \text{[because } \log_{10}(1000)=3\text{]}\\ \mathrm{dBm} &= 30 \end{aligned} \]

Watts–Milliwatts–dBm calculator
Enter one of the values, and click the Calculate button to compute the others.
Click Reset to enter a new value.
For the acoustic measurement of the total power radiated in all directions (referred to as Sound Power Level, or SWL), the same formula is used with a reference level correlating to the threshold of audibility mentioned earlier, 10-12 watts (also called a picowatt). Note how loud a sound with 1 watt of total acoustic energy might be at 120 dB SWL. This is the reported sound of a typical jet plane at 500 feet (whaaat, those four engines produce only 1 acoustic watt of sound? Yeah.).
\[ \begin{aligned} \mathrm{dB\ SWL} &= 10\log_{10}\!\left(\tfrac{1\,\mathrm{W}}{10^{-12}\,\mathrm{W}}\right)\\ \mathrm{dB\ SWL} &= 10\log_{10}\!\left(10^{12}\right) \quad \text{[that's some nifty math there]}\\ \mathrm{dB\ SWL} &= 10 \times 12 \quad \text{[because } \log_{10}(10^{12})=12\text{]}\\ \mathrm{dB\ SWL} &= 120 \end{aligned} \]

Acoustic Watts–Milliwatts–dB SWL Calculator
Enter one of the values, and click Calculate button to compute the others.
Click Reset to enter a new value.
Since intensity (I) at a fixed distance of measurement is directly proportional to power, a similar measurement can be made using a reference value of a picowatt per square meter (I = 10-12 W/m2) in place of Iref below to yield the Sound Intensity Level (SIL).
\[ I = 10 \log_{10}\!\left( \frac{I_1}{I_{\text{ref}}} \right)\,[\text{dB SIL}] \]
As a reminder, acoustic intensity is the measurement of power, or the rate at which energy passes through a defined area perpendicular to the direction of wave propagation. Thus, a ratio of power (watts) to area (square meters) is required, as demonstrated below.
As shown in the chart on the previous page, intensity is a measure of power present over or through an area. The following example calculates the acoustic intensity in dB SIL present at the surface of a loudspeaker with a cone radius of 0.5 meters receiving 1 watt of power. As stated, the common reference level for \( I_{\text{ref}} \) is \( 10^{-12} \ \text{W/m}^2 \).* Note the example below contains some rounding for clarity.
STEP 1: Find the area (A) of the speaker cone. The area of a circle is \( \pi r^2 \), so the cone area \( = \pi(0.5^2) = \pi × 0.25 \approx 0.78 \) square meters.
STEP 2: Compute the sound intensity in watts per square meter by dividing the applied power of 1 watt by the cone area of 0.78 m2. Thus, \( \frac{1}{0.78} \ \text{W/m}^2 \approx 1.28 \ \text{W/m}^2 \) yields the sound intensity at the surface of the speaker.
STEP 3: Compute the dB SIL using the STEP 2 sound intensity of \( 1.28 \ \text{W/m}^2 \) and the SIL reference value of \( 10^{-12} \ \text{W/m}^2 \) applied to the dB SIL formula above:
\[ \begin{aligned} I &= 10\log_{10}\!\left(\tfrac{1.28\,\mathrm{W/m^2}}{10^{-12}\,\mathrm{W/m^2}}\right)\ [\mathrm{dB\ SIL}]\\ I &= 10\log_{10}\!\left(1.28 \times 10^{12}\right)\ [\mathrm{dB\ SIL}]\\ I &\approx 10 \times 12.1\ [\mathrm{dB\ SIL}]\\ I &\approx 121\ \mathrm{dB\ SIL} \end{aligned} \]Consequently, 1 watt of power in terms of intensity I at the loudspeaker cone results in an approximately ear-splitting 121 dB SIL. This is very close to the 120 dB SWL calculated above using a 1-watt signal and the picowatt reference; the values would be even closer without rounding. As one moves farther away from the speaker and the sound field spreads out, this measurement changes dramatically at the surface of the sound sphere as the area (calculated in Step 1) increases geometrically. Incidentally, one might wonder why you'd buy a 500-watt amplifier if you can get an intensity of 121 dB out of a honking large speaker with only 1 watt of power. The sad fact is speakers are extremely inefficient at converting electrical power into acoustic power, so alas, only a small fraction of this energy is transferred.
*Thanks to David Howard and Jamie Angus, Acoustics and Psychoacoustics, 4th ed., 2009, for this example idea.